Download Extreme Optimization Numerical Libraries for .NET v8.1.9 (12 Sep 2022) + CRACK
- Home
- /
- Components
- /
- .Net
- /
- Other
What are Extreme Optimization Numerical Libraries for .NET?
The Extreme Optimization Numerical Libraries for .NET are an assortment of general-purpose mathematical and statistical classes designed specifically for Microsoft's Microsoft .NET Framework.
Extreme Optimization Numerical Libraries for .NET is a collection of general-purpose math and statistical courses. It is a complete statistical and technical computing platform built on the Microsoft .NET platform. It includes the math library, vector and matrix library, and a statistics library in a straightforward package.
Extreme Optimization Numerical Libraries for .NET Great Features:
General Features
- Easy to use even for the mathematically not-so-inclined.
- Excellent performance through optimized implementation of the best algorithms.
- Powerful enough to satisfy the most demanding power user.
- Intuitive object model. The objects in the Extreme Optimization Numerical Libraries for .NET and the relationships between them match our everyday concepts.
- Cross-platform. Works out-of-the-box on 32 and 64-bit platforms, .NET versions 1.1, 2.0, 3.0, and 3.5.
Math Library Features
- General
- Machine floating-point constants.
- Common mathematical constants.
- It extended elementary functions.
- Algorithm support functions: iteration, tolerance, convergence tests.
- Complex numbers
- Double-precision complex number value type.
- Overloaded operators for all arithmetic operations.
- Static operator functions for languages that don't support operator overloading.
- Extension of functions in the System.Math to the complex argument.
- Support for complex infinity and complex Not-a-Number (NaN).
- Complex vector and matrix classes.
- Numerical integration and differentiation
- Numerical differentiation.
- Numerical integration using Simpson's rule and Romberg's method.
- Non-adaptive Gauss-Kronrod numerical integrator.
- Adaptive Gauss-Kronrod numerical integrator.
- Integration over infinite intervals.
- Optimizations for functions with singularities and discontinuities.
- Six integration rules to choose from, or provide your own.
- Integration in 2 or more dimensions.
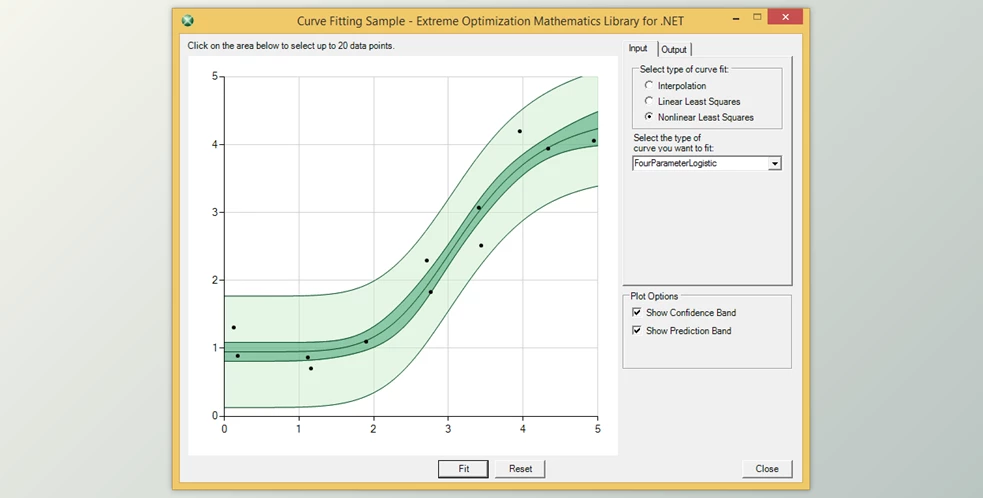
- Curve fitting and interpolation
- Interpolation using polynomials, cubic splines, piecewise constant, and linear curves.
- Linear least squares fit using polynomials or arbitrary functions.
- Nonlinear least squares using predefined functions or your own.
- Predefined nonlinear curves: exponential, rational, Gaussian, Lorentz, 4 and 5 parameter logistic.
- I weighted least squares with four predefined weight functions.
- I am scaling curve parameters.
- Constraints on curve parameters.
- Curves
- An object-oriented approach to working with mathematical curves.
- Methods for: evaluation, derivative, definite integral, tangent, roots.
- Many basic types of curves: constants, lines, quadratics, polynomials, cubic splines, Chebyshev approximations, and linear combinations of arbitrary functions.
- Solving equations
- Real and complex roots of polynomials.
- Roots of arbitrary functions: bisection, false positive, Dekker-Brent, and Newton-Raphson methods.
- Systems of simultaneous linear equations.
- Systems of nonlinear equations: Powell's hybrid 'dogleg' method, Newton's method.
- Least squares solutions.
- Optimization
- Optimization in 1 dimension: Brent's algorithm, Golden Section search.
- The quasi-Newton method in N dimensions: BFGS and DFP variants.
- Conjugate gradient method in N dimensions: Fletcher-Reeves and Polak-Ribière variants.
- Powell's conjugate gradient method.
- Downhill Simplex method of Nelder and Mead.
- Levenberg-Marquardt method for nonlinear least squares.
- Line search algorithms: Moré-Thuente, quadratic, unit.
- Linear program solver: Based on the Revised Simplex method.
- Linear program solver: Import from MPS files.
- Signal processing
- Accurate 1D and 2D Fast Fourier Transform.
- Complex 2D Fast Fourier Transform.
- Unique code for factors 2, 3, 4, and 5.
- Real and complex convolution.
- Managed 32bit and 64bit native implementations.
- Special functions
- Over 40 special functions are not included in the standard .NET Framework class library.
- Functions from combinatorics: factorial, combinations, variations, and more.
- Functions from number theory: greatest common divisor, least common multiple, decomposition into prime factors, primality testing.
- Gamma and related functions include incomplete and regularized digamma, beta, and harmonic numbers.
- Hyperbolic and inverse hyperbolic functions for real and complex numbers.
- Ordinary and Modified Bessel functions of the first and second kind.
- Airy functions and their derivatives.
- Exponential integral, sine and cosine integral, and logarithmic integral.
Vector and Matrix Library Features
- General
- Single, double, or quad precision absolute or complex components.
- Based on standard BLAS and LAPACK routines.
- 100% managed implementation for security, portability, and small sizes.
- Native, processor-optimized implementation for speed with large sizes based on the Intel® Math Kernel Library.
- Native 64bit support.
- GPU computing
- GPU computing: offload computations to the GPU.
- Data is kept on the GPU as long as possible for optimal performance.
- Vectors
- Dense vectors.
- Band vectors.
- Constant vectors.
- Row, column, and diagonal vectors.
- Vector views.
- Vector Operations
- Basic arithmetic operations.
- Element-wise operations.
- They overloaded arithmetic operators.
- Norms, dot products.
- Most significant and smallest values.
- Functions of vectors (sine, cosine, etc.)
- Matrices
- General matrices.
- Triangular matrices.
- Real symmetric matrices and complex Hermitian matrices.
- Band matrices.
- Diagonal matrices.
- Matrix views.
- Matrix Operations
- Basic arithmetic operations.
- Matrix-vector products.
- They overloaded arithmetic operations.
- Element-wise operations.
- Row and column scaling.
- Norms, rank, condition numbers.
- Singular values, eigenvalues, and eigenvectors.
- Matrix Decompositions
- LU decomposition.
- QR decomposition.
- Cholesky decomposition.
- Singular value decomposition.
- Symmetric eigenvalue decomposition.
- Non-symmetric eigenvalue decomposition.
- Banded LU and Cholesky decomposition.
- Sparse Matrices
- Sparse vectors.
- Sparse matrices.
- Matrices in Compressed Sparse Column format.
- Sparse LU Decomposition.
- Read matrices in Matrix Market format.
- Linear equations and least squares
- Shared API for matrices and decompositions.
- Determinants, inverses, numerical rank, condition numbers.
- Solve equations with one or multiple right-hand sides.
- Least squares solutions using QR or Singular Value Decomposition.
- Moore-Penrose Pseudo-inverse.
- Non-negative least squares (NNLS).
Statistics Library Features
- Descriptive Statistics
- Measures of central tendency: mean, median, trimmed mean, harmonic mean, geometric mean.
- Measures of scale: variance, standard deviation, range, interquartile range, absolute deviation from mean and median.
- Higher moments: skewness, kurtosis.
- Probability Distributions
- Probability density function (PDF).
- Cumulative distribution function (CDF).
- Percentile or inverse cumulative distribution function.
- Moments: mean, variance, skewness, and kurtosis.
- Generate random samples from any distribution.
- Parameter estimation for selected distributions.
- Continuous Probability Distributions
- Beta distribution.
- Cauchy distribution.
- Chi-squared distribution.
- Erlang distribution.
- Exponential distribution.
- F distribution.
- Gamma distribution.
- You generalized Pareto distribution.
- Gumbel distribution.
- Laplace distribution.
- Logistic distribution.
- Lognormal distribution.
- Normal distribution.
- Pareto distribution.
- Piecewise distribution.
- Rayleigh distribution.
- Student t distribution.
- She transformed beta distribution.
- She transformed gamma distribution.
- Triangular distribution.
- Uniform distribution.
- Weibull distribution.
- Discrete Probability Distributions
- Bernoulli distribution.
- Binomial distribution.
- Geometric distribution.
- Hypergeometric distribution.
- Negative binomial distribution.
- Poisson distribution.
- Uniform distribution.
- Multivariate Probability Distributions
- Multivariate normal distribution.
- Dirichlet distribution.
- Histograms
- One-dimensional histograms.
- Probability distribution associated with a histogram.
- General Linear Models
- Infrastructure for General Linear Model and Generalized Linear Model calculations.
- Analysis of variance.
- Regression analysis.
- Model-specific hypothesis tests.
- Analysis of variance (ANOVA)
- One and two-way ANOVA.
- One-way ANOVA with repeated measures.
- Regression analysis
- Simple, multiple, and polynomial regression.
- Nonlinear regression.
- Logistic regression.
- You generalized linear models.
- Flexible regression models.
- Variance-covariance matrix, regression matrix.
- Confidence intervals and significance tests for regression parameters.
- Time series analysis
- Treat several observation variables as a unit.
- Change the frequency of the time series.
- Automatically apply predefined aggregators.
- Advanced aggregators: volume weighted average.
- Transformations of Time Series Data
- It lagged time series, sums, and products.
- Change, percent change, growth rate.
- Extrapolated change, percent change, growth rate.
- Period-to-date sums and differences.
- Simple, exponential, weighted moving average.
- Savitsky-Golay smoothing.
- Multivariate Models
- Principal Component Analysis (PCA).
- Hierarchical clustering.
- K-means clustering.
- Statistical tests
- Tests for the mean: one sample z-test, one sample t-test.
- Paired and unpaired two-sample t-test for the difference between two sample means.
- Two Sample z-test for ratios.
- One sample chi-squared test for variance.
- F-test for the ratio of two variances.
- One and two sample Kolmogorov-Smirnov test.
- Anderson-Darling test for normality.
- Chi-squared goodness-of-fit test.
- Bartlett and Levene tests for homogeneity of variances.
- McNemar and Stuart-Maxwell test.
- Random number generation
- Compatible with the .NET Framework's System.Random.
- Four generators with varying quality, period, and speed to suit your application.
- Generate random samples from any distribution.
- Fauré and Halton sequences.
- Shufflers and randomized enumerators.
Click on the below link to download Extreme Optimization Numerical Libraries for .NET with CRACK NOW!
You are replying to :
Access Permission Error
You do not have access to this product!
Dear User!
To download this file(s) you need to purchase this product or subscribe to one of our VIP plans.
Files Password : DownloadDevTools.ir
Note
Download speed is limited, for download with higher speed (2X) please register on the site and for download with MAXIMUM speed please join to our VIP plans.
Discover free tools, limited-time offers, and stay updated with the latest software we release.







![FREE Download DevExpress Universal Complete [.Net Components] v25.2.3 (18 Dec 2025) + Documentation + Patcher](https://downloaddevtools.com/filemanagercontent/files/1/prolistnormal/124-banner.png)